1986 – 9(2)

Edmund Halley was nog geen dertig jaar oud toen hij Newton ervan overtuigde zijn boek te publiceren Principia (1686) zijn we hem een kaart van het aardmagnetisme verschuldigd, de hypothese van het dipoolmagnetisch veld, het idee om de zonneparallax te bepalen (evaluatie van de gemiddelde afstand tussen de zon en de aarde of de astronomische afstandseenheid) door observatie van de passages van de binnenplaneten, Mercurius en Venus, vóór de zonneschijf, daarnaast redigeerde hij de werken van Apollonius die handelden over de kegelsneden die zo nuttig zijn in de hemelmechanica. In 1679, toen hij door Kopenhagen trok, raakte hij bevriend met Hévélius, wiens observatiemethoden hij bestudeerde. Rond 1680 observeerde hij een komeet [[ Hoefer (Geschiedenis van de astronomie, 1873, blz. 461-462) schrijft deze gebeurtenis toe aan de komeet van 1681-1682 en meldt dat Halley deze heeft waargenomen “tijdens een reis naar Frankrijk”. Aan de andere kant Doublet (op. cit. blz. 334-335) legt deze reis vast in 1680 en schrijft: “hij was halverwege Calais en Parijs toen hij de beroemde komeet van 1680 opmerkte...”. In zijn Geschiedenis van de wetenschap (1965) ontleent Pierre Rousseau fragmenten van de twee auteurs die moeilijk met elkaar te verzoenen zijn: “… 1679… het jaar daarop… verscheen er een prachtige komeet… De harige ster ging voorbij en ging vervolgens verloren in de zonnestraling. In de tussentijd vertrok Halley in 1682 naar Frankrijk. Hij bevond zich halverwege Calais en Parijs toen hij een andere komeet zag, precies zoals de eerste, maar aan de andere kant van de zon passerend en precies tegenovergesteld. Als het hetzelfde was? vroeg hij zich af. Het kon niet hetzelfde zijn. Laten we terloops de vindingrijkheid bewonderen van het even onmogelijke ‘precies hetzelfde’. ]] waarvan Doerfel, leerling van Hevélius, de parabolische baan berekende en waarvan Newton aantoonde dat het een zeer langwerpige ellips kon zijn. We hadden daarom het recht om de periodiciteit van kometen en hun lidmaatschap van het zonnestelsel af te leiden. Halley paste de door Newton aanbevolen methode toe op vierentwintig reeksen komeetwaarnemingen die in het verleden waren gedaan. Hij identificeerde zich met de komeet van 1682, die hij had waargenomen, die van 1607, 1531 en waarschijnlijk 1456. Hij voorspelde (in 1704) de terugkeer ervan voor de jaren 1758-1759.

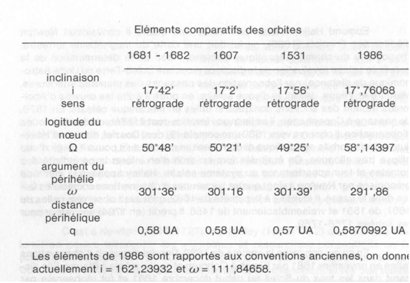
Wat de komeet van 1682 betreft, liet Doerfel in november 1681 waarnemingen doen door Kirsch in Coburg en door hemzelf in Plauen. Hij verdween begin december 1681 in het vuur van de zon en werd van eind december tot maart 1682 bij toeval opnieuw waargenomen aan de andere kant van de dagster. Hoewel vaak twee reeksen waarnemingen betrekking hadden op kometen die achter elkaar werden waargenomen vóór en achter de zon werd opgemerkt dat ze betrekking hadden op twee verschillende kometen (Képler schreef hun een rechtlijnige beweging toe). Doerfel kwam tot de overtuiging dat het dezelfde ster was waarvan hij de stijgende en dalende knooppunten vastlegde, door observatie, van de baan (dat wil zeggen de oriëntatie van het snijpunt van het baanvlak van de komeet ten opzichte van het vlak van de baan van de aarde, ecliptica). Halley berekende de nu historische elementen waarvan hij de identiteit evalueerde voor de komeet van 1607, waargenomen door Kepler en Longomontanus, en die van 1531 gerapporteerd door Apian, die hem overtuigden van de periodiciteit van ongeveer 76 jaar van het hemellichaam waarmee het nageslacht zijn naam verbonden.

In zijn voorspellingen voor de passage van 1758-1759 hield Halley geen rekening met de verstorende werking van de planeten op de beweging van ‘zijn’ komeet. Hij stelde de terugkeer naar het perihelium vast voor december 1758. Het was de wiskundige Alexis Clairaut (1713-1765) verbonden aan de rekenmachines Jérôme de Lalande en Hortense Lepaute [[ Hortense Lepaute, wiens De heiden van Galissière (1725-1792) keerde in 1771 terug uit India, na tevergeefs geprobeerd te hebben de passages van Venus voor de zon te observeren op 6 juni 1761 en 9 juni 1769, werd meter van de Hortensia.]] dat hij terugkeerde van het vaststellen van de theorie en het voorspellen van de overgang naar het perihelium voor 13 april 1759 [[Volgens Doublet zou het 3 april zijn (op. cit. P. 433). Maar J. Sauval (Hemel en aarde, vlucht. 101, 5-6, 1985, p. 210) specificeert een tussenpoos van tweeëndertig dagen. We kunnen denken dat het een typografisch omhulsel is (waarbij we 1 op 13 vergeten). ]]. Het vond feitelijk plaats op 12 maart. Het was de triomf van de Newtoniaanse mechanica!

De daaropvolgende ontdekking (1781) van de planeet Uranus door William Herschel (1738-1822) maakte het mogelijk om het waargenomen verschil van 32 dagen tussen voorspellingen en waarnemingen te interpreteren. Ter gelegenheid van de voor 1835 geplande terugkeer werd rekening gehouden met verstoringen als gevolg van Uranus. Damoiseau, Pontécoulant en Rosenberger brachten dit verschil terug tot vier dagen (16 november 1835). We weten vandaag dat dit kleine residu, dat in 1910 (drie dagen) nog steeds aanwezig was, kan worden verklaard door niet-zwaartekrachtinteracties, met name als gevolg van het verlies aan massa tijdens elke passage en door de rotatie van de komeetkern.