Het spel bestaat uit het gooien van een of twee dobbelstenen, het zoeken naar het verkregen getal in een tabel en het noteren ernaast van het getal van de meting waarmee het correspondeert. Menuetten, Polishes en trio's hebben aparte tabellen. We reproduceren dat van het eerste deel van de Polonaise, dat 6 maten heeft (fig. 9). Stel dat we 2 dobbelstenen hebben gegooid en dat we het getal 7 verkrijgen, zoeken we in de tweede rij beginnend vanaf de bovenkant (degene die de waarden van 2 tot 12 aangeeft die we kunnen verkrijgen met 2 dobbelstenen) het getal 7; in rij 1 dobbelstenen lezen we onder het getal 7 het getal 72. Dit laatste verwijst naar de maat waarop dit getal staat. Als de tweede worp het getal 4 oplevert, zal het nummer van de tweede maat genoteerd in rij 2 Die onder het getal 4 8 zijn. Ervan uitgaande dat de volgende worpen 10 (= maat nr. 143), 8 (= 87) opleveren, 3 (= 52) en 12 (= 154), zouden we het Pools van figuur 10 verkrijgen.
Dobbelstenentafel, voor de Polonoifes, voor het eerste spel.
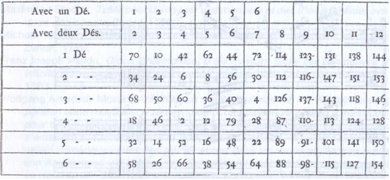
Tabel met getallen voor het samenstellen van polijstmiddelen van 6 maten met behulp van één of twee dobbelstenen, overgenomen van Johann Philipp KIRNBERGER, De kunst van het ter plekke samenstellen van menuetten en poetsmiddelen, Berlijn 1757.
We begrijpen dat alle maten die overeenkomen met de dobbelstenen van rij 1 (70, 10, 42, 62, 44, etc.) zo moeten worden geschreven dat ze kunnen worden gekoppeld aan elke maat van de dobbelstenen van rij 2 (34, 24, 6, 8, 38, enz.), dat deze op hun beurt moeten kunnen worden gekoppeld aan elke maat van rij 3 dobbelstenen (68, 50, 60, 36, enz.), enzovoort. Hetzelfde geldt voor de cellen van twee maten waaruit het thema bestaat, en voor de zeven variaties die naast elkaar op de cilinders van het Componium staan vermeld. Terwijl in de set van Kirnberger de cellen uit één enkele meting bestaan; op de Componium hebben de cellen twee maten, wat de mogelijkheid openlaat om binnen de twee maten een paar kleine vluchtige modulaties uit te voeren, voordat je terugkeert naar de leidtoon. Als je zorgvuldig alle genummerde maten onderzoekt die op de 29 muziekpagina's voorkomen, besef je dat Kirnberger feitelijk een Pools en een Menuet heeft gecomponeerd met elk 10 variaties; Vervolgens segmenteerde hij de verschillende varianten en camoufleerde alles in een digitale tabel. Alle menuetten zijn in D majeur, met een constante en identieke harmonische progressie. De trio's na de menuetten zijn in D mineur en voldoen aan dezelfde eisen voor harmonische uniformiteit. In werkelijkheid biedt alleen de methode echte verandering. Er zijn in totaal 116 combinaties voor de 6-maats polijstmiddelen; 11 8 combinaties voor de 8-maats polijstmiddelen; 11 32 mogelijkheden voor menuetten met trio's. L. Ratner wijst erop dat de gehele bevolking van Europa een leven lang de stukken had kunnen spelen zonder de combinaties uit te putten [[L. RATNER, op. cit., P. 344. ]]. Kirnberger zelf vroeg een wiskundige genaamd Gumpertz om het aantal combinaties te berekenen dat geproduceerd kon worden en hij kwam tot het resultaat van 1 biljoen.Waarschuwing bovenaan het boek gepubliceerd. Het is niet verrassend dat de musicoloog Charles Burney Kirnberger ervan beschuldigde “ambitieuzer te zijn wat betreft het karakter van een algebraïst dan een geniale muzikant” (Ch. BURNEY, De huidige stand van de muziek in Duitsland, Nederland en de Verenigde Provinciën, T. II, Londen, 1775, p. 213). ]].

Voorbeeld van Pools verkregen door het muzikale spel van J. Ph. Kirnberger.
Een soortgelijk spel, uitgegeven in Parijs in 1758 onder de titel Ludus melothedicus of harmonisch dez-spel, gaat nog een stap verder in de fragmentatie, waarbij niet langer elke maat, maar elke noot wordt geïsoleerd.