
Cercle entier, XVIIe s., inv. 4036
Diam. 15 cm
© Musées royaux d’Art et d’Histoire




Qui ?
Le cercle entier est décrit pour la première fois par Gemma Frisius (1508-1555), en 1533, dans son ouvrage Libellus de locorum describendorum ratione. Muni d’une boussole, cet instrument sera plus tard appelé « cercle hollandais » par erreur par le colonel Laussedat qui décrit Gemma Frisius (1508-1555) aux Hollandais.
Quand ?
Les premières traces écrites de cet instrument datent de 1533. Il est utilisé jusqu’au XVIIIe siècle, quand il est remplacé par d’autres instruments plus précis, munis d’optiques.
Évolution :
Un des plus grands contributeurs au perfectionnement du cercle sur pied est l’abbé Picard (1620-1682), co-créateur de l’Académie royale des Sciences de Paris. Son apport est le remplacement du réticule de visée classique par une lunette dotée d’une mire. Il semble que le perfectionnement de ce type de mire, ainsi que son usage à des fins de visée, soit dû à Cornelio Malvasia (1603-1664) en 1662.
Le cercle entier est à l’origine d’autres instruments, tels le graphomètre et le théodolite.
Pour quoi ?
Le cercle entier, cercle sur pied, ou encore (parfois) cosmolabe, est un instrument composé d’un plan circulaire gradué et divisé en 360 ° surmonté d’une lunette ou d’une mire. Il permet de mesurer l’angle formé entre deux points distants en les reportant, pour en mesurer la distance. Son principe de fonctionnement, ponctuel, permet d’en faire un usage aussi bien terrestre (géodésique ou d’arpentage par la triangulation) que céleste (calcul de position entre des astres).
Cet instrument est, par sa forme et son fonctionnement, proche de l’astrolabe, dont il dérive.
Comment ?
L’instrument fonctionne comme suit :
- Un cercle, d’un diamètre général de 15 cm à 1 pied, placé à l’horizontale est surmonté d’une ligne de visée.
- Le premier point est visé à travers ladite ligne de visée.
- La distance angulaire entre l’organe de visée et un méridien fixe est mesurée.
- Le second point est visé à travers la ligne de visée.
- De nouveau, la distance angulaire est mesurée. Il suffit dès lors de reporter l’angle sur le cercle, et de lire la valeur indiquée.

Exemple d’utilisation non-terrestre :
Ailleurs, par exemple en astronomie, son usage est analogue à celui du théodolite à l’horizontal. Le cercle s’y utilise comme un cercle azimutal, qui, et c’est là sa spécificité, peut déterminer l’angle entre deux astres dont il est toutefois nécessaire de connaître l’élévation. L’axe nord-sud faisant, ici, figure de méridien de référence.
Comme l’indique le schéma suivant :
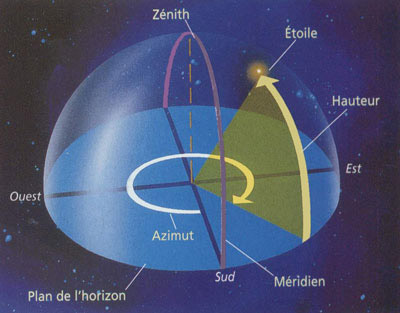
Le principe de fonctionnement reste, autrement, le même.
Œuvres liées :
Références :
BESSON J., Le Cosmolabe ou Instrument universel concernant toutes observations qui se peuvent faire par les sciences mathématiques, tant au ciel, en la terre, comme en la mer de l’invention de M. Jacques Besson... ; [Le Cosmographe instrument adjoinct en la supérieure partie du cosmolabe au lieu de l’atlas]3 – 1567
BREZINSKI Cl., Les images de la terre. Cosmographie, géodésie, topographie et cartographie à travers les siècles, Paris, 2010, p. 275-276
MORIZET M., Les instruments de levée topographique à l’époque du Vauban dans Progrès et immobilisme (Recueil d’articles du Comité International de Cartographie ), 2008, (Consulté le 01 décembre 2011)
REBOUX O., Mesurer l’inaccessible. Arpentage et géométrie pratique
http://fr.wikipedia.org/wiki/Jean_Picard:
http://theses.univ-lyon2.fr/documents/getpart.php?id=lyon2.2005.guilhot_n&part=312371
http://fr.wikipedia.org/wiki/Th%C3%A9odolite.















