De wetenschap waarop deze architect-ingenieurs uit de Middeleeuwen in wezen trots zijn, is de geometrie. Vaak proberen we deze geometrie van hen te karakteriseren door te zeggen dat er, in tegenstelling tot die van Euclides, geen demonstraties bij betrokken zijn. Maar dat is niet het probleem.
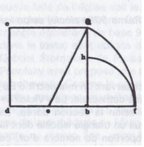
Er bestond in de Middeleeuwen een hele stroming van praktische geometrieën, die zowel voortkwamen uit de Romeinse agrimens als uit het gebruik van het astrolabium of de wijzerplaat. Deze verhandelingen bevatten over het algemeen geen demonstraties en toch zijn ze heel anders dan wat we bijvoorbeeld aantreffen in Villard de Honnecourt en zijn opvolger Master II. Voor dit laatste wordt de geometrie gereduceerd tot een soort puur visuele en operationele recepten, die niet alleen demonstraties, maar vooral ook berekeningen uitsluiten. Als symbool van deze gemoedstoestand reproduceerde ik de representatie van ԉ door Matthäus Roriczer (Fig. 1).
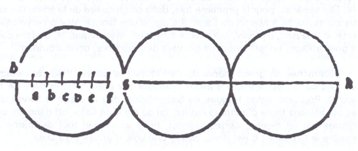
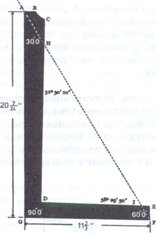
Eens, in 1963, kreeg ik de gelegenheid om te bestuderen wat er in 1391 gebeurde op de bouwplaats van de kathedraal van Milaan. Het ging erom het gebouw zo op te trekken dat de top van de kerk de top zou vormen van een gelijkzijdige driehoek waarvan de basis de breedte van het monument zou zijn. Concreet ging het om het berekenen van de hoogte van een gelijkzijdige driehoek met basis 96. Geconfronteerd met een dergelijk probleem, hebben ingenieurs (inzignerii in de tekst) zijn verplicht een beroep te doen op een “expert in de kunst van de geometrie”, Gabriel Stornaloro van Piacenza. Op basis van deze berekening stelde de grote kunsthistoricus Erwin Panofsky een uiterst gecompliceerde en vergezochte reconstructie voor. Net als het geheim van de alchemisten of het geheim van de grote maritieme ontdekkingen, lijkt het zogenaamde ‘geheim van de bouwmeesters’ vaak de meest extravagante wetenschappelijke praatjes aanvaardbaar te maken. In het geval van de Dom van Milaan werd in feite eenvoudigweg de in de Middeleeuwen gebruikelijke formule toegepast, volgens welke de hoogte van een gelijkzijdige driehoek 26/30 van de basis bedraagt. Maar opnieuw waren de ingenieurs niet in staat deze berekening uit te voeren en moesten ze een deskundige landmeter te hulp roepen. Hoewel de geometrie van de architect-ingenieurs uit de 13e eeuw niet berekende, wist ze toch uit verschillende instrumenten, in het bijzonder het vierkant, bronnen te putten die tot voor kort onvermoed bleven. Kijk naar het plein met niet-parallelle randen, waarvan de architect Hughes Libergier uit Reims de contouren ervan op zijn eigen graf had getekend. Een langs de hypotenusa gespannen touw lijkt de twee hoeken te verschaffen die worden gevormd door de diagonaal van een rechthoek waarvan de twee zijden de verhouding van de gulden snede daartussen hebben (fig. 2).
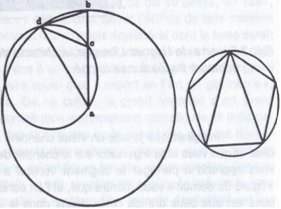
We vinden in Villard de Honnecourt verschillende van deze pleinen met niet-parallelle randen. Ze zouden tegelijkertijd kunnen worden gebruikt om de gewelfelementen door te snijden en, bij gebrek aan een gradenboog op dat moment, het direct verkrijgen van bevoorrechte hoeken en relaties mogelijk te maken. Echter, tussen dergelijke praktijken en Elementen van Euclides is het ijzeren gordijn misschien minder onbegaanbaar dan mensen zeggen. Dat dacht ik tenminste toen ik in Salamanca de Wiskunde van een Toulouse-geleerde uit de 14e eeuw, Philippe Eléphant, werd ik ertoe gebracht belangstelling te krijgen voor de merkwaardige namen die soms aan de Middeleeuwen worden toegeschreven, voor bepaalde figuren uit Elementen van Euclides. Kijk naar de figuren genaamd "Victory" en "Demon Figure" (Fig. 3).